Trees : Introduction to Data Structures and Algorithms

What is a Tree?

A tree is a nonlinear data structure. It is a collection of nodes where each node contains addresses of other nodes. A tree data structure has a root node, internal nodes and leaf nodes. The number of children of a node determines the type of tree i.e. if a node contains addresses of two other nodes, it is a binary tree.

There are various types of trees namely binary tree, binary search tree, B tree, B+ Tree and some complex trees like Red-Black trees and AVL trees.

Why use Trees?

Trees have a variety of applications. Some of them are as follows:

Syntax trees and annotated parse trees are used in compiler design for every program we compile.
A priority queue scheduling follows a heap data structure which is a kind of tree.
A tree-based data structure “Trie” is used in contact management systems.
Sets in C++ are implemented using Binary Search Tree

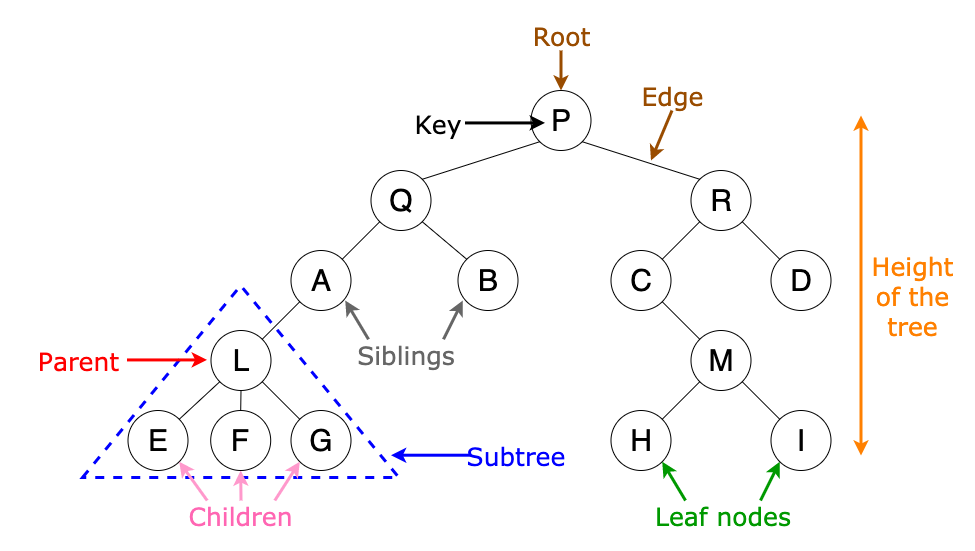
Terminologies you might come across while exploring trees

Root node: The topmost node in the tree

Leaf node: The bottommost nodes are the leaf nodes. They do not have any children

Child: If a node is a descendant of any node, it is called a child node

Internal node: A node with at least one child is an internal node

Depth(Height): The vertical distance of a node from the root is called the depth of that node

Types of Tree Traversals:

Tree traversal has three basic types:

Inorder: Here the root node appears in between the left and right node
Preorder: Here the root node appears before the left and right node
Postorder: Here the root appears after the left and right node

Here is the code to implement these traversals.

#include <bits/stdc++.h>
using namespace std;

//Making a tree node to store the tree's value and its children
class Node
{
    public:

    int data;
    Node* left; //left children 
    Node* right; // right children


    Node(int val)
    {
        data = val;
    }
};

void inorder(Node* root)
{
    if(root==NULL)
        return;

    inorder(root->left);
    cout<<root->data<<" ";
    inorder(root->right);

}
void preorder(Node* root)
{
    if(root==NULL)
        return;


    cout<<root->data<<" ";
    preorder(root->left);
    preorder(root->right);

}
void postorder(Node* root)
{
    if(root==NULL)
        return;

    postorder(root->left);
    postorder(root->right);   
    cout<<root->data<<" ";

}

int main()
{

    struct Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);

    cout<<"\nThe inorder traversal is as follows : \n";
    inorder(root);

    cout<<"\nThe preorder traversal is as follows : \n";
    preorder(root);

    cout<<"\nThe postorder traversal is as follows : \n";
    postorder(root);
}

Binary Tree vs Binary Search Tree

A binary tree has data representation in a hierarchical format whereas a binary search tree has data representation in an ordered format.
A binary tree allows duplicate values whereas Binary search trees do not allow duplicate values.

Note: The inorder traversal of a binary search tree is sorted

Conclusion

Tree data structure is a very important concept from an interview perspective. Some coding questions you should try are listed below.

Striver's Link: https://takeuforward.org/data-structure/strivers-tree-series-tree-data-structure/

Image credits : Vijini Mallawaarachchi(https://towardsdatascience.com/8-useful-tree-data-structures-worth-knowing-8532c7231e8c)

Trees : Introduction to Data Structures and Algorithms | Topic - 2

Table of contents